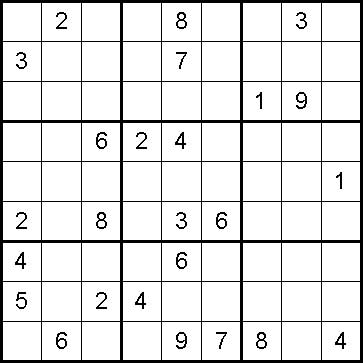
Sudoku je populární logická hra, jejímž cílem je na plochu 9x9 polí doplnit chybějící číslice 1-9 takovým způsobem, aby se žádná neopakovala vícekrát v žádném řádku, sloupci ani čtverci (plocha se skládá z devíti čtverců velikosti 3x3 pole).
Autorem hlavolamu je Howard Garns, který jej publikoval v roce 1979 (pod názvem Number place). Hra se stala populární nejprve v Japonsku (vydávána od roku 1984) pod názvem Suuji wa dokushin ni kagiru a v roce 2005 se stala známou na celém světě.
Jak řešit Sudoku?
Sudoku se obvykle luští za pomoci tzv. kandidátů, což jsou všechna čísla, která mohou být v daném poli umístěna (na začátku všechna čísla 1-9). Kandidáti jsou poté postupně eliminováni za pomoci více či méně složitých myšlenkových postupů a konstrukcí. V okamžiku, kdy zbyde pouze jeden kandidát, tak je řešením pro dané pole.
Základní pravidla
Pro prvotní eliminaci kandidátů poslouží základní pravidla Sudoku. V žádné řádce, sloupci ani skupině nesmí být žádné číslo vícekrát. Ačkoliv je tato strategie velmi jednoduchá, tak postačuje pro většinu jednoduchých Sudoku.
(Hidden) Singles
Singles jsou ta políčka, pro která existuje pouze jeden kandidát, který je jejich řešením. Hidden single je takový kandidát, který je jedinečný v rámci dané řádky, sloupce nebo skupiny, ale není v daném políčku osamocený. Přesto je díky základním pravidlům řešením tohoto políčka.
Naked pair
Pokud dvě políčka v rámci skupiny obsahují pouze totožnou dvojici kandidátů, pak žádné další pole v této skupině nesmí dané kandidáty obsahovat (pokud by tomu tak nebylo, tj. některý kandidát by byl řešením jiného pole, tak by nešlo původní políčka vyplnit). Tuto strategii lze analogicky použít pro trojice kandidátů a tři políčka, čtveřice a čtyři políčka a tak dále.
Pointing pairs, Pointing tripples (intersection removal)
Za předpokladu, že se některý kandidát vyskytuje vícekrát v rámci jednoho řádku nebo sloupce skupiny (ale ne v rámci více sloupců/řádků), tak jej můžeme odstranit z průsečíku tohoto řádku/sloupce v ostatních skupinách, kterými tento řádek/sloupec prochází.
Box/Line reduction (intersection removal)
Pokud předchozí postup obrátíme naruby, tak dostaname Box/Line reduction strategii. Mějme řádek nebo sloupec, který má určité kandidáty pouze v jedné skupině, pak můžeme tyto kandidáty vyškrtnout ze všech ostatních polí dané skupiny.
Strojové řešení a generování Sudoku
Při generování nového zadání je zapotřebí řešit Sudoku ve dvou rovinách. Tou první je ověření jednoznačnosti zadání, které provedeme pomocí backtrackingu. Backtracking je metoda organizovaných pokusů a omylů, při které zkusíme na dané pole vložit nějakou hodnotu a zkontrolujeme, jestli toto částečné řešení neodporuje pravidlům. Pokud je vše v pořádku, zkusíme to znovu u dalšího pole. V případě selhání se vrátíme na místo posledního omylu a opravíme jej novým pokusem. Tímto způsobem zaručeně najdeme všechna řešení, která zadání umožňuje. Nevýhodou je velká výpočetní náročnost tohoto postupu (ručně by se dala tato metoda aplikovat jen na velmi omezené podproblémy).
Druhou rovinou je ověření praktické řešitelnosti daného Sudoku. To provedeme pouze za pomoci lidmi použitelných technik, z nichž některé jsme uvedli výše. Tímto způsobem také můžeme snadno stanovit obtížnost řešení na základě počtu potřebných tahů nebo obtížnosti nutných strategií.
Generování zadání
V předchozích odstavcích jsme předpokládali existenci zadání, ale neuvedli jsme si, jakým způsobem jej lze získat. V praxi se používají především dva postupy. První z nich vygeneruje náhodné konzistentní úplné řešení Sudoku a postupně z něj odebírá vyplněná řešení jednotlivých polí. Takto postupuje tak dlouho, dokud má Sudoku jednoznačné řešení, případně dokud obtížnost řešení nepřesáhne nějaký práh.
Druhý přístup je zcela opačný. Algoritmus nejprve vygeneruje zadání, v němž je konzistentně vyplněno 17 polí (nejmenší známý počet polí, pro nějž bylo nalezeno zadání, které má unikátní řešení). Poté procedura postupně vyplňuje náhodná pole a kontroluje konzistenci zadání. V okamžiku, kdy má dané zadání pouze jedno řešení, jehož obtížnost nepřesáhne daný práh, procedura terminuje.
Kód
/**
* Resic Sudoku pomoci backtrackingu. Tato metoda nezjisti, jestli je dane
* sudoku resitelne clovekem, ale zda-li ma dane zadani vubec reseni, pripadne
* kolik takovychto reseni umoznuje (zjisti a vypise vsechna reseni).
* @author Pavel Micka
*/
public class SudokuSolver {
/**
* Velikost ulohy == klasicke Sudoku 9*9, 3x vnitrni ctverec 3*3, kazde cislo
* (1-9) pouze jednou v radku, sloupci i ctverci
*/
public static final int SUDOKU_SIZE = 9;
/**
* Velikost vnitrnich ctvercu (3*3 dle beznych pravidel)
*/
public static final int SQUARE_SIZE = 3;
/**
* Prazdne pole
*/
public static final int EMPTY = 0;
/**
* Vyresi zadane Sudoku pomoci backtrackingu (najde vsechna reseni)
* @param array pole zadani
*/
public static void solveSudoku(int[][] array) {
if(array.length != SUDOKU_SIZE) throw new IllegalArgumentException("Pole ma mit velikost 9x9");
boolean[][] fixed = new boolean[SUDOKU_SIZE][SUDOKU_SIZE];
for (int i = 0; i < array.length; i++) {
if (array[i].length != SUDOKU_SIZE) throw new IllegalArgumentException("Pole ma mit velikost 9x9");
for (int j = 0; j < array.length; j++) {
if (array[i][j] != 0) fixed[i][j] = true;
}
}
//prejdeme na prvni nepredvyplnenou souradnici
int x = -1;
int y = 0;
do {
x = x + 1; //posun o souradnici dal
boolean overflow = x >= SUDOKU_SIZE; //pretekl radek?
if (overflow) {
x = 0;
y += 1;
}
} while(fixed[y][x]); //dokud je pole zablokovane (soucasti zadani)
for (int i = 1; i <= SUDOKU_SIZE; i++) {
solve(array, fixed, x, y, i);
}
}
/**
* Resi Sudoku
* @param array pole reseni
* @param fixed pole, ve kterem true znamena, ze jde o hodnotu ze zadani,
* @false, ze jde o hodnotu resitele
* @param x souradnice x, na kterou se bude pridavat dalsi hodnota
* @param y souradnice y, na kterou se bude pridavat dalsi hodnota
* @param value hodnota
*/
private static void solve(int[][] array, boolean[][] fixed, int x, int y, int value) {
if (!checkConsistency(array, x, y, value)) return; //reseni neni konzistentni
array[y][x] = value; //set
do {
x = x + 1; //posun o souradnici dal
boolean overflow = x >= SUDOKU_SIZE; //pretekl radek?
if (overflow) {
x = 0;
y += 1;
if (y == SUDOKU_SIZE) { //pretekl sloupec...konec reseni
printArray(array);
return;
}
}
} while(fixed[y][x]);//dokud je pole zablokovane (soucasti zadani)
for (int i = 1; i <= SUDOKU_SIZE; i++) { //backtrack
solve(array, fixed, x, y, i);
}
array[y][x] = EMPTY; //reset policka (aby neprekazelo pri backtracku)
}
/**
* Zkontroluje, jestli je reseni stale korektni
* @param array pole reseni
* @param x x souradnice, na kterou je pridavana hodnota
* @param y y souradnice, na kterou je pridavana hodnota
* @param value hodnota
* @return true - pokud je reseni konzistentni, false - pokud reseni neni konzistentni
*/
private static boolean checkConsistency(int[][] array, int x, int y, int value) {
//Sloupec
for (int i = 0; i < array.length; i++) {
if (i != y && array[i][x] == value) return false;
}
//radek
for (int i = 0; i < array[y].length; i++) {
if (i != x && array[y][i] == value) return false;
}
//ctverec
int vertical = y/SQUARE_SIZE; //o kolikaty vertikalni ctverec se jedna
int horizontal = x/SQUARE_SIZE; //o kolikaty horizontalni ctverec se jedna
for (int i = vertical*SQUARE_SIZE; i < vertical*SQUARE_SIZE + SQUARE_SIZE; i++) {
for (int j = horizontal*SQUARE_SIZE; j < horizontal*SQUARE_SIZE + SQUARE_SIZE; j++) {
if (array[i][j] == value) return false;
}
}
return true;
}
/**
* Vypise pole Sudoku
* @param array pole sudoku
*/
private static void printArray(int[][] array) {
for (int i = 0; i < array.length; i++){
for (int j = 0; j < array[i].length; j++) {
System.out.print(array[i][j] + "|");
}
System.out.println("");
}
System.out.println("");
}
}
/**
* Resicka sudoku vyuzivajici "lidske" strategie
* @author Pavel Micka
*/
public class HumanizedSudokuSolver {
private SudokuField[][] sudoku;
private SudokuStrategy[] strategies;
/**
* Zkonstruuje resicku pro zadane sudoku
* @param setting zadani sudoku, 0 znaci prazdne pole
* @param strategies pole strategii, ktere maji byt pouzity
*/
HumanizedSudokuSolver(int[][] setting, SudokuStrategy... strategies) {
this.strategies = strategies;
sudoku = new SudokuField[setting.length][setting.length];
for (int i = 0; i < setting.length; i++) {
for (int j = 0; j < setting[i].length; j++) {
if (setting[i][j] == 0) {
sudoku[i][j] = new SudokuField();
} else {
sudoku[i][j] = new SudokuField(setting[i][j]);
}
}
}
}
/**
* Vrati reseni sudoku
* @return
*/
public int[][] solve() {
boolean succ;
do{
succ = false;
for (SudokuStrategy s : strategies) {
succ = s.solve(sudoku);
if (succ) {
break;
}
}
} while(succ);
int[][] solution = new int[sudoku.length][sudoku.length];
for (int i = 0; i < sudoku.length; i++) {
for (int j = 0; j < sudoku.length; j++) {
solution[i][j] = sudoku[i][j].getSolution();
}
}
return solution;
}
/**
* Testovaci main metoda
* Program vyresi, co umi, coz jsou s temito strategiemi cca. az pokrocila
* Sudoku a vypise vysledek
* @param args the command line arguments
*/
public static void main(String[] args) {
int[][] setting = { //MF DNES 23.8.2010, priloha leto
{0, 0, 4, 0, 3, 6, 9, 2, 7},
{1, 0, 0, 0, 0, 5, 0, 0, 0},
{0, 0, 0, 2, 0, 0, 0, 0, 4},
{0, 0, 5, 0, 0, 0, 0, 6, 0},
{6, 4, 0, 0, 0, 0, 0, 8, 5},
{0, 7, 0, 0, 0, 0, 2, 0, 0},
{5, 0, 0, 0, 0, 1, 0, 0, 0},
{0, 0, 0, 7, 0, 0, 0, 0, 2},
{4, 3, 7, 9, 2, 0, 5, 0, 0}
};
SudokuStrategy[] s = {new OneInARowStrategy(), new OneInAColumnStrategy(), new OneInAGroupStrategy()};
HumanizedSudokuSolver solver = new HumanizedSudokuSolver(setting, s);
int[][] solution = solver.solve();
for (int i = 0; i < solution.length; i++) {
for (int j = 0; j < solution.length; j++) {
System.out.print(solution[i][j] + " ");
}
System.out.println("");
}
}
}
/**
* Specifikuje metodu, kterou by mely mit vsechny strategie pro reseni Sudoku
* @author Pavel Micka
*/
interface SudokuStrategy {
/**
* Provede jeden krok reseni Sudoku
* @param sudoku pole obsahujici sudoku, 0 oznacuje prazdna mista
* @return true pokud se povedlo krok provest, false v opacnem pripade
*/
public boolean solve(SudokuField[][] sudoku);
}
/**
* Strategie, ktera rika, ze v jednom radku smi byt dane cislo pouze jednou
* @author Pavel Micka
*/
class OneInARowStrategy implements SudokuStrategy {
public boolean solve(SudokuField[][] sudoku) {
for (int i = 0; i < sudoku.length; i++) {
for (int j = 0; j < sudoku[i].length; j++) {
int solution = sudoku[i][j].getSolution();
if (solution != 0) { //pokud pole neni vyreseno
for (int k = 0; k < sudoku[i].length; k++) { //overme radku na kandidaty
if (sudoku[i][k].getSolution() == 0) { //pokud dane pole neni vyreseno
if (sudoku[i][k].hasCandidate(solution)) { //a pokud ma kandidata
sudoku[i][k].removeCandidate(solution); //tak kandidata odstranime
System.out.println("OneInARow: Odstranuji kandidata " + solution
+ " na souradnicich x: " + k + " y: " + i);
return true; //a vratime uspech
}
}
}
}
}
}
return false;
}
}
/**
* Strategie, ktera rika, ze v jednom sloupci smi byt dane cislo pouze jednou
* @author Pavel Micka
*/
class OneInAColumnStrategy implements SudokuStrategy {
public boolean solve(SudokuField[][] sudoku) {
for (int i = 0; i < sudoku.length; i++) {
for (int j = 0; j < sudoku[i].length; j++) {
int solution = sudoku[j][i].getSolution();
if (solution != 0) { //pokud pole neni vyreseno
for (int k = 0; k < sudoku.length; k++) { //overme sloupec na kandidaty
if (sudoku[k][i].getSolution() == 0) { //pokud dane pole neni vyreseno
if (sudoku[k][i].hasCandidate(solution)) { //a pokud ma kandidata
sudoku[k][i].removeCandidate(solution); //tak kandidata odstranime
System.out.println("OneInAColumn: Odstranuji kandidata " + solution
+ " na souradnicich x: " + i + " y: " + k);
return true; //a vratime uspech
}
}
}
}
}
}
return false;
}
}
/**
* Strategie, ktera rika, ze v jedne skupine muze byt dane cislo pouze jednou
* @author Pavel Micka
*/
class OneInAGroupStrategy implements SudokuStrategy {
public boolean solve(SudokuField[][] sudoku) {
int groupCount = (int) Math.sqrt(sudoku.length); //pocitame se ctvercovym sudoku, pocet skupin na radku a sloupec
for (int i = 0; i < sudoku.length; i++) {
for (int j = 0; j < sudoku[i].length; j++) {
int solution = sudoku[i][j].getSolution();
if (solution != 0) { //pokud pole neni vyreseno
for (int k = i - (i % groupCount); k < i - (i % groupCount) + groupCount; k++) {//radky
for (int l = j - (j % groupCount); l < j - (j % groupCount) + groupCount; l++) {//sloupce
if (sudoku[k][l].getSolution() == 0){ //pokud pole jeste neni vyreseno
if (sudoku[k][l].hasCandidate(solution)){ //a ma odpovidajiciho kandidata
sudoku[k][l].removeCandidate(solution);
System.out.println("OneInAGroup: Odstranuji kandidata " + solution
+ " na souradnicich x: " + l + " y: " + k);
return true;
}
}
}
}
}
}
}
return false;
}
}
/**
* Trida policka sudoku
* @author Pavel Micka
*/
class SudokuField {
/**
* Mnozina kandidatu
*/
private Set<Integer> candidates;
/**
* Vytvori policko, kandidaty jsou cisla 1-9
*/
public SudokuField() {
this.candidates = new HashSet<Integer>();
for (int i = 1; i <= 9; i++) {
candidates.add(i);
}
}
/**
* Vytvori policko s jedinym kandidatem (resenim)
* @param nr reseni
*/
public SudokuField(int nr) {
this.candidates = new HashSet<Integer>();
candidates.add(nr);
}
/**
* Zjisti, jestli je dane cislo kandidatem tohoto pole
* @param nr cislo
* @return true pokud je cislo kandidatem, false jinak
*/
public boolean hasCandidate(int nr) {
return candidates.contains(nr);
}
/**
* Odstrani kandidata
* @param nr kandidat
*/
public void removeCandidate(int nr) {
boolean succ = candidates.remove(nr);
assert succ;
}
/**
* Vrati cislo, ktere je resenim tohoto policka
* @return cislo, ktere je resenim, 0 pokud jeste pole nebylo vyreseno
*/
public int getSolution() {
if (candidates.size() != 1) {
return 0;
} else {
return (Integer) (candidates.toArray()[0]);
}
}
}
/**
* Resic Sudoku pomoci backtrackingu. Tato metoda nezjisti, jestli je dane
* sudoku resitelne clovekem, ale zda-li ma dane zadani vubec reseni, pripadne
* kolik takovychto reseni umoznuje (zjisti a vypise vsechna reseni).
* @author Pavel Micka
*/
class SudokuSolver {
public:
/**
* Velikost ulohy == klasicke sudoku 9*9, 3x vnitrni ctverec 3*3, kazde cislo
* (1-9) pouze jednou v radku, sloupci i ctverci
*/
static const int SUDOKU_SIZE = 9;
/**
* Velikost vnitrnich ctvercu (3*3 dle beznych pravidel)
*/
static const int SQUARE_SIZE = 3;
/**
* Prazdne pole
*/
static const int EMPTY = 0;
/**
* Vyresi zadane Sudoku pomoci backtrackingu (najde vsechna reseni)
* @param array pole zadani
*/
static void solveSudoku(int ** array) {
bool ** fixed = new bool *[SUDOKU_SIZE];
for (int i = 0; i < SUDOKU_SIZE; i++) {
fixed[i] = new bool[SUDOKU_SIZE];
}
for (int i = 0; i < SUDOKU_SIZE; i++) {
for (int j = 0; j < SUDOKU_SIZE; j++) {
if (array[i][j] != 0) fixed[i][j] = true;
else fixed[i][j] = false;
}
}
//prejdeme na prvni nepredvyplnenou souradnici
int x = -1;
int y = 0;
do {
x = x + 1; //posun o souradnici dal
bool overflow = x >= SUDOKU_SIZE; //pretekl radek?
if (overflow) {
x = 0;
y += 1;
}
} while (fixed[y][x]);//dokud je pole zablokovane (soucasti zadani)
for (int i = 1; i <= SUDOKU_SIZE; i++) {
solve(array, fixed, x, y, i);
}
//dealokace
for (int i = 0; i < SUDOKU_SIZE; i++) delete fixed[i];
delete[] fixed;
}
private:
/**
* Resi Sudoku
* @param array pole reseni
* @param fixed pole, ve kterem true znamena, ze jde o hodnotu ze zadani,
* @false, ze jde o hodnotu resitele
* @param x souradnice x, na kterou se bude pridavat dalsi hodnota
* @param y souradnice y, na kterou se bude pridavat dalsi hodnota
* @param value hodnota
*/
static void solve(int ** array, bool ** fixed, int x, int y, int value) {
if (!checkConsistency(array, x, y, value)) return; //reseni neni konzistentni
array[y][x] = value; //set
do {
x = x + 1; //posun o souradnici dal
bool overflow = x >= SUDOKU_SIZE; //pretekl radek?
if (overflow) {
x = 0;
y += 1;
if (y == SUDOKU_SIZE) { //pretekl sloupec...konec reseni
printArray(array);
return;
}
}
} while(fixed[y][x]);//dokud je pole zablokovane (soucasti zadani)
for (int i = 1; i <= SUDOKU_SIZE; i++) { //backtrack
solve(array, fixed, x, y, i);
}
array[y][x] = EMPTY; //reset policka (aby neprekazelo pri backtracku)
}
/**
* Zkontroluje, jestli je reseni stale korektni
* @param array pole reseni
* @param x x souradnice, na kterou je pridavana hodnota
* @param y y souradnice, na kterou je pridavana hodnota
* @param value hodnota
* @return true - pokud je reseni konzistentni, false - pokud reseni neni konzistentni
*/
static bool checkConsistency(int ** array, int x, int y, int value) {
//Sloupec
for (int i = 0; i < SUDOKU_SIZE; i++) {
if (i != y && array[i][x] == value) return false;
}
//radek
for (int i = 0; i < SUDOKU_SIZE; i++) {
if (i != x && array[y][i] == value) return false;
}
//ctverec
int vertical = y/SQUARE_SIZE; //o kolikaty vertikalni ctverec se jedna
int horizontal = x/SQUARE_SIZE; //o kolikaty horizontalni ctverec se jedna
for (int i = vertical*SQUARE_SIZE; i < vertical*SQUARE_SIZE + 3; i++) {
for (int j = horizontal*SQUARE_SIZE; j < horizontal*SQUARE_SIZE + 3; j++) {
if (array[i][j] == value) return false;
}
}
return true;
}
/**
* Vypise pole Sudoku
* @param array pole sudoku
*/
static void printArray(int ** array) {
for (int i = 0; i < SUDOKU_SIZE; i++) {
for (int j = 0; j < SUDOKU_SIZE; j++) {
cout << array[i][j] << "|";
}
cout << "\\n";
}
cout << "\\n";
}
};
Litaratura
- STUART, Andrew. Sudokuwiki.org/ [online]. 2008 [cit. 2010-08-24]. Dostupné z WWW: <http://www.sudokuwiki.org/>.
- JOHNSON, Angus. Angus johnson's homepage [online]. 2005 [cit. 2010-08-24]. SOLVING SUDOKU. Dostupné z WWW: <http://www.angusj.com/sudoku/hints.php>.