Dijkstrův algoritmus je nejrychlejší známý algoritmus pro nalezení všech nejkratších cest ze zadaného uzlu do ostatních uzlů grafu, který neobsahuje hrany záporné délky. Algoritmus byl vymyšlen nizozemským informatikem Edsgerem Dijkstrou v roce 1959.
Princip
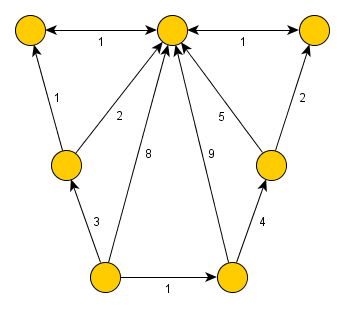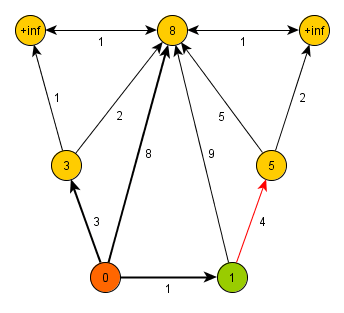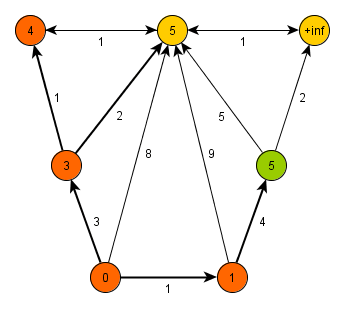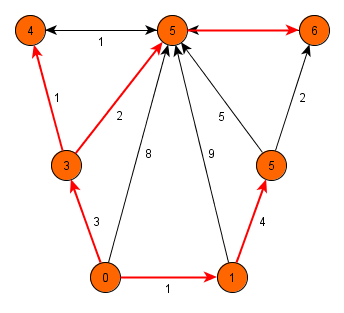
Na Dijkstrův algoritmus lze pohlížet jako na zobecněné prohledávání grafu do šířky, při kterém se vlna nešíří na základě počtu hran od zdroje, ale vzdálenosti od zdroje (ve smyslu váhy hran). Tato vlna proto zpracovává jen ty uzly, k nimž již byla nalezena nejkratší cesta.
Dijkstrův algoritmus si uchovává všechny uzly v prioritní frontě řazené dle vzdálenosti od zdroje - v první iteraci má pouze zdroj vzdálenost 0, všechny ostatní uzly nekonečno. Algoritmus v každém svém kroku vybere z fronty uzel s nejvyšší prioritou (nejnižší vzdáleností od již zpracované části) a zařadí jej mezi zpracované uzly. Poté projde všechny jeho dosud nezpracované potomky, přidá je do fronty, nejsou-li tam již obsaženi, a ověří, zda-li nejsou blíže zdroji, než byli před zařazením právě vybraného uzlu mezi zpracované. To znamená, že pro všechny potomky ověřuje:
Pokud nerovnost platí, tak danému potomkovi nastaví novou vzdálenost a označí za jeho předka zpracovávaný uzel. Po průchodu přes všechny potomky algoritmus vybere z fronty uzel s nejvyšší prioritou a celý krok opakuje.
Algorimus terminuje v okamžiku, kdy jsou zpracovány všechny uzly (prioritní fronta je prázdná).
Dijkstrův algoritmus je použitelný jen tehdy, obsahuje-li graf pouze nezáporně ohodnocené hrany - v opačném případě není schopen garantovat, že při zpracování uzlu byla již nalezena nejkratší možná cesta.
Složitost
Složitost Dijkstrova algoritmu závisí na implementaci prioritní fronty. V případě její implementace pomocí sekvenčního vyhledávání je složitost algoritmu , při použití binární haldy
.
Kód
/**
* Dijkstruv algoritmus
* @param d matice delek, pozice [0 1] = 2 znamena, ze z uzlu 0 vede do uzlu 1 hrana delky 2
* @param from uzel ze ktereho se hledaji nejkratsi cesty
* @return strom predchudcu (z ciloveho uzlu znaci cestu do uzlu from)
*/
procedure int[] doDijkstra(d, from) {
//vlozi vsechny prvky do prioritni fronty (radi vzestupne dle vzdalenosti), uzel from ma vzdalenost 0, vsechny ostatni nekonecno
Q = InsertAllNodesToTheQueue(d, from)
CLOSED = {} //uzevrene uzly - prazdna mnozina
predecessors = new array[d.nodeCount] //pole predchudcu
while !Q.isEmpty() do
//vrat uzel v nejnizsi vzdalenosti a odstan jej z fronty
node = Q.extractMin()
CLOSED.add(node) //uzavri uzel
//zkrat vzdalenosti
for a in Adj(node) do //pro vsechny potomky uzlu
if !CLOSED.contains(a) //pokud jiz nebyl potomek uzavren
//pokud se pridanim uzlu vzdalenost potomka snizila
if Q[node].distance + d[node][a] < Q[a].distance
//zmen prioritu (vzdalenost) uzlu
Q[a].distance = Q[node].distance + d[node][a]
//zmen predka uzlu a na node
predecessors[a] = node
return predecessors
/**
* Dijkstruv algoritmus
* @param d matice delek (Integer.MAX_VALUE pokud hrana mezi uzly neexistuje)
* @param from uzel ze ktereho se hledaji nejkratsi cesty
* @return strom predchudcu (z ciloveho uzlu znaci cestu do uzlu from)
*/
public static int[] doDijkstra(int[][] d, int from) {
Set<Integer> set = new HashSet<Integer>();
set.add(from);
boolean[] closed = new boolean[d.length];
int[] distances = new int[d.length];
for (int i = 0; i < d.length; i++) {
if (i != from) {
distances[i] = Integer.MAX_VALUE;
} else {
distances[i] = 0;
}
}
int[] predecessors = new int[d.length];
predecessors[from] = -1;
while (!set.isEmpty()) {
//najdi nejblizsi dosazitelny uzel
int minDistance = Integer.MAX_VALUE;
int node = -1;
for(Integer i : set){
if(distances[i] < minDistance){
minDistance = distances[i];
node = i;
}
}
set.remove(node);
closed[node] = true;
//zkrat vzdalenosti
for (int i = 0; i < d.length; i++) {
//existuje tam hrana
if (d[node][i] != Integer.MAX_VALUE) {
if (!closed[i]) {
//cesta se zkrati
if (distances[node] + d[node][i] < distances[i]) {
distances[i] = distances[node] + d[node][i];
predecessors[i] = node;
set.add(i); // prida uzel mezi kandidaty, pokud je jiz obsazen, nic se nestane
}
}
}
}
}
return predecessors;
}
Literatura
- KOLÁŘ, Josef. Teoretická informatika. 2. vyd. Praha : Česká informatická společnost, 2004. 205 s. ISBN 80-900853-8-5.