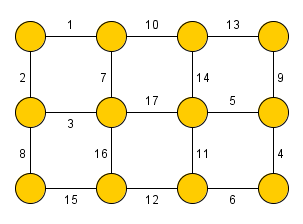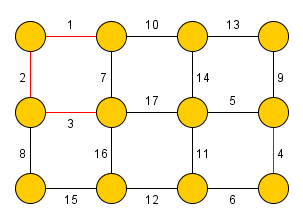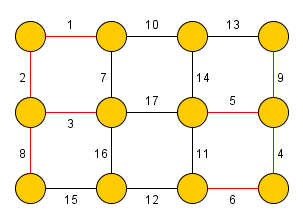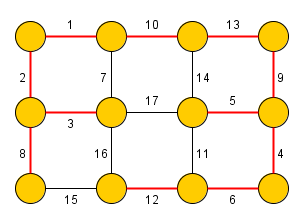
Kruskalův algoritmus

Kruskalův algoritmus slouží k nalezení minimální kostry grafu (kostry takové, že součet vah jejích hran je minimální). Algoritmus byl poprvé publikován v roce 1956 Josephem Kruskalem.

Princip

Kruskalův algoritmus nejprve setřídí hrany dle jejich váhy (od nejmenší) a následně přidává hrany do grafu takovým způsobem, aby nevznikl žádný cyklus (tj. procedura terminuje po přidání $\\vert U \\vert -1$ hran).

K zajištění acykličnosti si algoritmus pomocí datové struktury disjoint set udržuje pro každý uzel informaci o příslušnosti ke komponentě souvislosti. Disjoint set poskytuje dvě operace: union (spojí dvě komponenty souvislosti) a find (zjistí pro daný uzel příslušnost ke komponentě souvislosti).

Asymptotická složitost algoritmu

Časová složitost algoritmu je v případě použití řadicího algoritmu založeného na porovnávání $O(\\vert H\\vert \\cdot \\log \\vert H \\vert)$ . Pokud jsou hrany již předřazeny, nebo je možno k jejich seřazení použít řadicí algoritmus s lineární složitostí (např. counting sort), tak je složitost Kruskalova algoritmu rovna $O(\\vert H\\vert \\cdot \\alpha(\\vert H \\vert))$ , kde $\\alpha$ je inverzní Ackermannova funkce (odpovídá složitosti operací union a find).

/**
 * Kruskaluv algoritmus
 * @param graph graf
 * @param w vahy jednotlivych hran
 * @return minimalni kostra grafu
 */
SpanningTree kruskalAlgorithm(Graph graph, weights w)
    SpanningTree tree //kostra
    for Node n : graph do
        makeSet(n) //kazdy uzel je v samostatnem setu
    List edges = sort(graph.getEdges(), w) //seradi hrany podle vah
     
    for Edge e in edges do
        if findSet(e.start) != findSet(e.end) //pokud jsou pocatecni a koncovy uzel v ruznych setech (netvorime cyklus)
            tree.add(e) //pridej hranu do kostry
            union(e.start, e.end) //sety spojime v jeden
            if tree.edgeCount() == graph.nodeCount() - 1 //pokud uz je kostra cela
                break //konec pridavani hran
    return tree

/**
 * Kruskaluv algoritmus
 * @author Pavel Micka
 */
public class KruskalAlgorithm {
    /**
     * Nalezne minimalni kostru neorientovaneho grafu o n uzlech (cisla uzlu
     * 0, 1, ..., n-1)
     * @param edges hrany neorientovaneho grafu
     * @param nodeCount pocet uzlu neorientovaneho grafu (n)
     * @return minimalni kostra
     */
    public static List<Edge> kruskalAlgorithm(List<Edge> edges, int nodeCount) {
        DisjointSet ds = new DisjointSet(nodeCount);
        List<Edge> spanningTree = new ArrayList<Edge>();
        Collections.sort(edges);
        int i = 0;
        while (i != edges.size() && spanningTree.size() != nodeCount - 1) {
            Edge e = edges.get(i);
            if(ds.find(e.getFrom()) != ds.find(e.getTo())){
                spanningTree.add(e);
                ds.union(e.getFrom(), e.getTo());
            }
            i++;
        }
        return spanningTree;
    }
}
 
 
// ***************************** //
// *     DATOVE STRUKTURY      * //
// ***************************** //
 
 
/**
 * Hrana neorientovaneho grafu
 * @author Pavel Micka
 */
class Edge implements Comparable<Edge> {
    private int from; //uzel z
    private int to; //uzel do
    private int weight; //vaha
    public Edge(int from, int to, int weight) {
        this.from = from;
        this.to = to;
        this.weight = weight;
    }
    /**
     * Provede porovnani hran dle vahy (vyssi vaha == vetsi)
     * @param o
     * @return
     */
    public int compareTo(Edge o) {
        if (this.getWeight() > o.getWeight()) {
            return 1;
        } else if (this.getWeight() < o.getWeight()) {
            return -1;
        } else {
            return 0;
        }
    }
 
    /**
     * @return the from
     */
    public int getFrom() {
        return from;
    }
 
    /**
     * @param from the from to set
     */
    public void setFrom(int from) {
        this.from = from;
    }
 
    /**
     * @return the to
     */
    public int getTo() {
        return to;
    }
 
    /**
     * @param to the to to set
     */
    public void setTo(int to) {
        this.to = to;
    }
 
    /**
     * @return the weight
     */
    public int getWeight() {
        return weight;
    }
 
    /**
     * @param weight the weight to set
     */
    public void setWeight(int weight) {
        this.weight = weight;
    }
}
/**
 * Jednoducha implementace Union-Find problemu
 * @author Pavel Micka
 */
class DisjointSet {
 
    private Node[] nodes;
 
    public DisjointSet(int nodeCount) {
        nodes = new Node[nodeCount];
        for (int i = 0; i < nodeCount; i++) {
            nodes[i] = new Node();
            nodes[i].id = i;
        }
    }
 
    /**
     * Provede sjednoceni komponent, ve kterych jsou uzly "a" a "b"
     * Union provadi vzdy do A
     * @param a cislo uzlu a
     * @param b cislo uzlu b
     * @return cislo reprezentanta sjednocene komponenty
     */
    public int union(int a, int b) {
        Node repA = nodes[find(a)];
        Node repB = nodes[find(b)];
 
        repB.parent = repA;
        return repA.id;
    }
 
    /**
     * Vrati reprezentanta zadaneho uzlu
     * @param a cislo uzlu, jehoz reprezentanta hledame
     * @return cislo reprezentanta uzlu
     */
    public int find(int a) {
        Node n = nodes[a];
        int jumps = 0;
        while (n.parent != null) {
            n = n.parent;
            jumps++;
        }
        if (jumps > 1) repair(a, n.id);
        return n.id;
    }
 
    /**
     * Provede opravu (compression) cesty
     * @param a
     * @param rootId
     */
    private void repair(int a, int rootId) {
        Node curr = nodes[a];
        while (curr.id != rootId) {
            Node tmp = curr.parent;
            curr.parent = nodes[rootId];
            curr = tmp;
        }
    }
 
    @Override
    public String toString() {
        StringBuilder builder = new StringBuilder();
        for (int i = 0; i < nodes.length; i++) {
            builder.append(find(i) + " ");
        }
        return builder.toString();
    }
 
    /**
     * Uzel n-arniho stromu
     */
    private static class Node {
        /**
         * Rodic
         */
        Node parent;
        /**
         * Identifikator uzlu
         */
        int id;
    }
}

Literatura

KOLÁŘ, Josef. Teoretická informatika. 2. vyd. Praha : Česká informatická společnost, 2004. 205 s. ISBN 80-900853-8-5.

Princip

Asymptotická složitost algoritmu

Kód

Literatura

Doporučujeme