Jarník-Primův algoritmus

Jarník-Primův algoritmus (Jarníkův algoritmus, Primův algorimus, Prim-Jarníkův algorimus, DJP algorithm) slouží k určení minimální kostry grafu (kostra taková, že součet vah jejíchž hran je minimální). Tento algoritmus byl vynalezen v roce 1930 českým matematikem Vojtěchem Jarníkem a v roce 1957 znovu nezávisle objeven americkým matematikem Robertem Primem. Algorimus byl opět objeven v roce 1959 Edsgerem Dijkstrou.

Princip

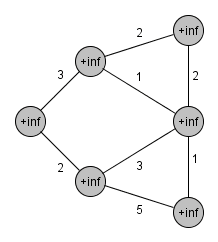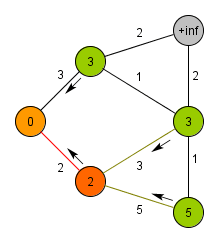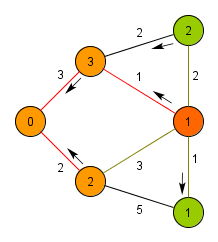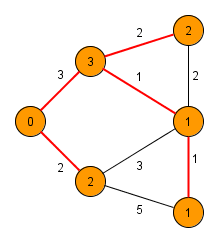
Algoritmus vychází z libovolného uzlu a udržuje si seznam již objevených uzlů a jejich vzdáleností od propojené části grafu. V každém svém kroku připojí ten z uzlů, mezi nímž a projenou částí grafu je hrana nejnižší délky a označí sousedy nově připojeného uzlu za objevené, případně zkrátí vzdálenosti od již známých uzlů, pokud byla nalezena výhodnější hrana. V okamžiku, kdy jsou propojeny všechny uzly, algoritmus terminuje.

Složitost

Složitost Jarník-Primova algoritmu závisí na konkrétní implementaci seznamu. Seznam samotný může být modifikován při každém objevení nové hrany (tj. $\\vert H \\vert$ krát), jelikož vždy může dojít buď k objevení dosud neznámého uzlu nebo ke změně vzdálenosti některého již objeveného uzlu. Pokud budeme seznam implementovat pomocí binární haldy, jež se chová jako prioritní fronta, tak každá z operací modifikace seznamu bude mít asymptotickou složitost $O(\\log_{2}{\\vert U \\vert})$ . Celková asymptotická složitost Jarník-Primova algoritmu je proto $O(\\vert H \\vert \\cdot \\log_{2}{\\vert U \\vert})$ .

Kód

Pseudocode

/**
 * Jarnik-Primuv algoritmus
 * Nalezne minimalni kostru grafu
 * @graph graf 
 * @weight vahy hran  
 * @return pole predchudcu  
 */
node[] jarnikAlgorithm(graph, weight)
    Queue q //fronta
    q.addAllVetices(graph.vertices) //pridej vsechny uzly do fronty
     
    distances = new int[q.size()] //pole vzdalenosti
    distances[0] = 0 //koren
    for i in 1 -> distances.length - 1 do                                
        distances[i] = +inf //ostatni uzly jsou nekonecne daleko
      
    predecessors = new node[q.size()] //pole predchudcu
    predecessors[0] = null //koren nema predchudce
     
    while !queue.empty() do //dokud neni fronta prazdna
        u = queue.extractMin() //vrat prvek v minimalni vzdalenosti
        for node in descendants(u) do //pro vsechny potomky u
            if queue.contains(node) AND weight(u, node) < d[node] //pokud se nektery z potomku priblizil k dosud postavene kostre
                then predecessors[node] = u //u je tedy jeho predek
                     d[node] = weight(u, node) //nastav nvou vzdalenost    
     
    return predecessors //vrat pole predchudcu

Literatura

KOLÁŘ, Josef. Teoretická informatika. 2. vyd. Praha : Česká informatická společnost, 2004. 205 s. ISBN 80-900853-8-5.

Princip

Složitost

Kód

Literatura

Doporučujeme