Borůvkův algoritmus slouží k nalezení minimální kostry grafu (kostry takové, že je součet vah jejích hran minimální). Byl vymyšlen českým matematikem Otakarem Borůvkou za účelem nalezení efektivního trasování elektrické sítě na Moravě. Algoritmus byl později několikrát znovuobjeven (mezi jinými M. Sollinem), proto se o něm lze dočíst také jako o Sollinově algoritmu.
Princip
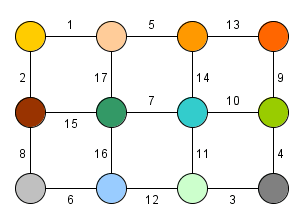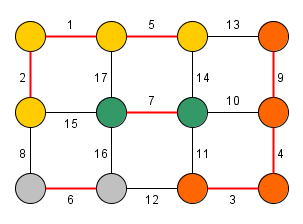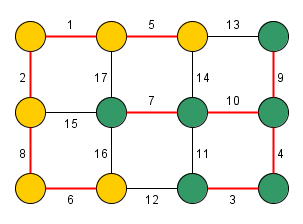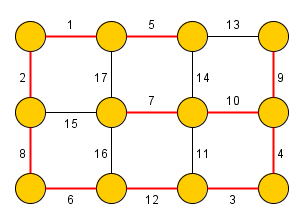
Borůvkův algorimus funguje na principu skládání komponent. Na začátku jsou všechny uzly grafu považovány za samostatné komponenty. Algoritmus v každém svém kroku propojí každou komponentu s jinou komponentou pomocí nejkratší možné hrany. Jelikož Borůvkův algoritmus vyžaduje, aby měly všechny hrany unikátní váhu, tak při propojení komponent nikdy nemůže vzniknout cyklus. Dále je zajištěno, že se v každém kroku zmenší počet komponent minimálně na polovinu - tj. algoritmus terminuje v krocích. Při každém z těchto kroků je třeba najít pro všechny komponenty nejkratší vycházející hranu, což může zabrat až
operací. Celková
asymptotická složitost Borůvkova algoritmu je tedy
).
Paralelizace algoritmu
Významnou výhodou Borůvkova algoritmu je snadná paralelizace spojování jednotlivých komponent řešení. Protože vyhledávání nejlevnějších hran vycházejících z daných komponent je zcela nezávislé na stavu ostatních komponent, tak lze tyto podproblémy řešit na samostatných výpočetních jednotkách.
Kód
/**
* Boruvkuv algoritmus
* V teto podobe nesnese graf s dvema stejne ohodnocenymi hranami
* @param graph graf
* @param weight vahy jednotlivych hran
* @return minimalni kostra
*/
boruvkaAlgorithm(graph, weight)
SpanningTree tree //kostra
components = graph.vertices //na pocatku jsou vrcholy nepospojovany
while components.size > 1 do
for each component in components //pro vsechny komponenty
edge e = connectWithMinimalEdge(component, weight) //propojime s jinou komponentou pomoci minimalni hrany
tree.add(e) //hranu pridame do kostry
return tree
SEO od společnosti Digital Pylon
Online casino s algoritmem
České casino online online slot-vegas.cz
Hrajte nejlepší hry jako je GoodGame Empire.
Zajímavé články: Jak najít práci snů? Zvolte kariéru v IT!, Češi mají rádi hrací automaty online, Jak funguje algoritmické obchodování Casino, Online výuka Algoritmus a online marketing mají svá pravidla, Automaty, Matematický vliv, Ratings, Jak fungují algoritmy hazardních her online: více znalostí, více peněz, SYPWAI - nástroj pro vědecký vývoj, Vynikají na globálním trhu: Nejlepší vývojáři softwaru pro online výherní automaty, Jak si vybrat nejlepší české online casino, Proč byste měli hrát online casino VPN revoluce, Kde najdeme algoritmy v každodenním životě?, Čeká vás pracovní pohovor mimo město? Podívejte se, jak dokonale zvládnout včasný příchod, 5 úžasných technologií ze světa hazardních her, Mirror and access to Mostbet, Svou kancelář můžete mít stále po ruce, Jaké výhody má digitalizovaná firma oproti off-line konkurenci?, Jaký systém vybrat pro snadné řízení výroby?, Nahradí umělá inteligence ajťáky?, Důvody, proč používat SnapTik ke stahování videí TikTok, Dokonalý den na pláži: Co si vzít s sebou, aby byl výlet zábavný a bezpečný?, Jak přežít dlouhý let?, Go pay GoodGame Empire, Blockchain, Rozhovor, Umělá inteligence, Ochranná známka pre softvér: Prečo ju registrovať?, Role kryptografických algoritmů v zabezpečení online kasin, Jaké jsou náklady na nákup 3D tiskárny?, Jak algoritmy vylepšují online zážitky v roce 2025, Epilace laserem a péče o pokožku před a po ní, Byty k pronájmu Sokolov - výhody a rizika pronájmu bytu bez realitky, Filmy a seriály plné hádanek: kryptografie jako hlavní téma, Kdy obnovit data z disku běžně dostupným softwarem a kdy už se obrátit na profesionály?, Jak se zbavit jizev po akné? Co z domácí péče opravdu funguje? Na co všechno se zaměřit při výběru internetového připojení pro firmy?, Promo kód casino: mezi matematikou bonusů a českou realitou