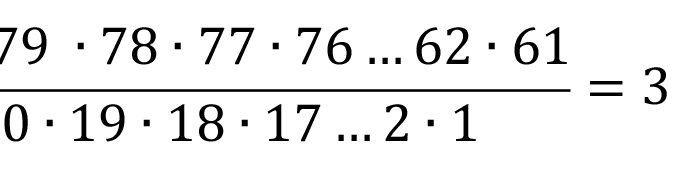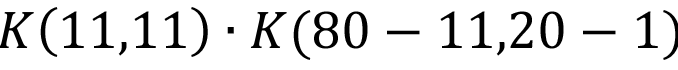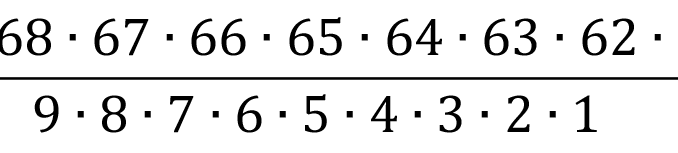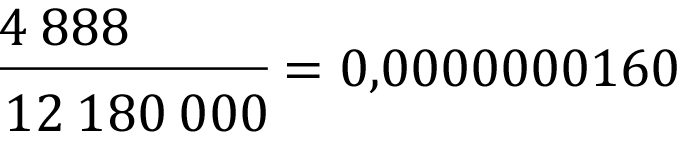Každou k-tici z n-prvků, v níž nezáleží na pořadí, a ve které se každý prvek vyskytuje maximálně jednou, nazveme kombinací.
Počet všech kombinací bez opakování můžeme vyjádřit následujícím vzorcem.
Kde je počet k-členných variací z n prvků. Výraz nejvíce vpravo čteme n nad k a nazýváme jej kombinačním číslem.
Kombinační číslo
Pro každé kombinační číslo platí:
Dále také platí:
Kombinace s opakováním
Za předpokladu, že umožníme, aby se jednotlivé prvky opakovaly až k-krát (tj. až do maximálního počtu prvků), tak hovoříme o k-členné kombinaci s opakováním. Počet všech kombinací s opakováním lze vypočítat jako:
Příklad
Vypište všechny dvoučlenné kombinace (bez opakování) prvků .
Řešení
Příklad
Vypište všechny dvoučlenné kombinace s opakováním prvků .
Řešení
Příklad
Vypočtěte hodnotu kombinačního čísla .
Řešení
Příklad
V loterijní hře Sportka tipuje soutěžící 6 čísel ze 49. U tažených čísel nezáleží na pořadí, každé číslo může být vylosováno maximálně jednou.
Hlavní výhru získá hráč, který správně označí všechna čísla. Jakou šanci na hlavní výhru má hráč, který si vsadí jeden sloupeček (tj. má jeden tip)?
Řešení
Počet možností, kterými mohou výt čísla vylosována, vypočítáme jako kombinaci 6 prvků ze 49 bez opakování.
Šance na výhru je rovna počtu tipů děleno počtem možností.
Hráč získá hlavní výhru s pravděpodobností 0,000007151123%.
Příklad
V obchodě prodávají 5 druhů cukroví. Kolika způsoby lze nakoupit 16 kusů cukroví?
Řešení
Jedná se o kombinaci s opakováním (jednotlivé druhy můžeme nakoupit vácekrát).
Cukroví lze nakoupit 232560 způsoby.
Kód
/** Autor: Vaclav Kejr */
public long KombinaceBezOpakovani(int k, int n)
{
try
{
long kombinace = 0;
if (n >= 2 && n <= 10 && k >= n)
{
int a = n + k - 1;
kombinace = this.Faktorial(a) / (this.Faktorial(k) * this.Faktorial(n - 1));
}
return kombinace;
}
catch (SystemException ex)
{
Console.WriteLine(ex.ToString());
return -1;
}
}
public long KombinaceOpakovani(int k, int n)
{
try
{
long kombinaceOpakovani = 0;
if (k >= 2 && k <= 10 && n >= 2 && n <= 10)
{
int a = n + k - 1;
int b = n - 1;
kombinaceOpakovani = this.Faktorial(a) / (this.Faktorial(k) * this.Faktorial(b));
}
return kombinaceOpakovani;
}
catch (SystemException ex)
{
Console.WriteLine(ex.ToString());
return -1;
}
}
public long Faktorial(int n)
{
try
{
long faktor = 1;
if (n < 1)
{
throw new ArgumentException("Argument n < 1 !", n.ToString());
}
else if (n == 1)
{
return faktor = 1;
}
else if (n >= 2 && n <= 20)
{
for (int i = 2; i <= n; i++)
{
faktor *= i;
}
return faktor;
}
else
{
throw new ArgumentException("Argument n > 20 !", n.ToString());
}
}
catch (SystemException ex)
{
Console.WriteLine(ex.ToString());
return -1;
}
}
Příklad
V dalším komplikovanějším příkladu se podíváme na loterijní hru Zlatých 11, kde se táhne celkem 20 čísel 80. Cílem hráče je pak trefit 11 z těchto tažených 20. Jakou šanci má hráč trefit hlavní výhru, tedy 11 z 20 tažených.
Řešení
Počet možností, kterými mohou výt čísla vylosována, vypočítáme jako kombinaci 20 prvků z 80 bez opakování.
V dalším kroku je nutné vypočítat počet možných kombinací, kdy tipneme všech 11 z 11 při 20 slosovaných číslech.
Podle definice pravděpodobnosti nyní musíme porovnat všechny příznivé možností s celkovými možnými.
Hráč získá hlavní výhru s pravděpodobností 0,00000160302707334508 %.
Literatura
- POLÁK, Josef. Přehled středoškolské matematiky. 8. vydání. Praha 4 : Prometheus, 2005. 608 s.