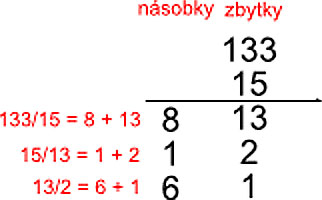Euklidův algoritmus, který byl uveřejněn řeckým matematikem Euklidem v knize základy cca 300 let př.n.l., slouží k nalezení nejvyššího společného dělitele dvou čísel (značíme gcd – greatest common divisor), jeho rozšířená verze pak i k nalezení multiplikativní inverze čísla .
Princip
Mějme dvě čísla – 133 a 15, jejich nejvyšší společný dělitel nalezneme takto:
133 vydělíme se zbytkem patnácti. Nyní si musíme uvědomit tyto věci. Jak levá, tak pravá strana rovnice musí být dělitelná gcd (protože hledáme gcd 133 a 15 a obě strany jsou 133). Dalším poznatkem je, že násobek patnácti je nevýznamný, protože gcd je faktorem samotného čísla 15, čili násobek klidně můžeme vynechat. Posledním a nejdůležitějším poznatkem je, že pokud gcd dělí 15 a zároveň je celá pravá strana dělitelná gcd, tak i zbytek (v našem případě 13) musí být dělitelný gcd.
Když všechna tato pravidla poskládáme, tak z nich plyne, že dělení se zbytkem můžeme opakovat pro redukovaná čísla. Jelikož se levá strana vždy musí zmenšit a nemůže klesnout na 0, tak algoritmus terminuje a levá strana je jeho variantem. Další postup je proto analogický s prvním krokem, pouze na nižsích číslech:
Nyní, když nám vyšel zbytek 0, tak již vidíme, které nejvyšší číslo dělí jak levou, tak pravou stranu, je to číslo 1 (protože z předchozího kroku jsme věděli, že námi hledané číslo musí dělit čísla 2 a 1).
Příklad 2 – čísla 140 a 15:
Nejvyšším společným dělitelem čísel 140 a 15 je číslo 5.
Kód
/**
* Vstup: Čísla a > 0, b > 0
* Výstup: gcd(a, b)
*/
function gcd(a, b)
if a >= b then
m = a
n = b
else
m = b
n = a
while n != 0 do
m = p*n + z
m = n
n = z
return m
/**
* Returns greatest common divisor of the given numbers
* @param a number 1
* @param b number 2
* @return gcd(a, b)
*/
public static int gcd(int a, int b) {
if (a < 1 || b < 1) throw new IllegalArgumentException("a or b is less than 1");
while (b != 0) {
int tmp = a;
a = b;
b = tmp % b;
}
return a;
}
Rozšířený Euklidův algoritmus
Rozšířená verze Euklidova algoritmu umožňuje nalézt multiplikativní inverzi na tělese Zp, kde p je prvočíslo. Není nezbytně nutné, aby se jednalo o těleso, ale v takovém případě nemáme zaručeno, že inverze bude vůbec existovat.
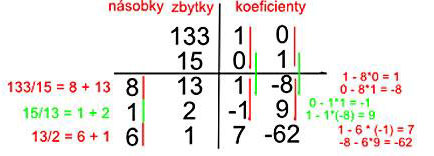
Rozeberme si princip opět na prvním příkladu:
Nalezněte multiplikativní inverzi čísla 15 v Z133. Předpokládejme, že je 1, protože jinak by multiplikativní inverze neexistovala. Vždy se nyní snažíme rozepsat zbytky tak, aby byly vyjádřeny jako součet násobků čísel 133 a 15. Proto očekáváme, že v posledním kroku vyjde rovnost ve tvaru
, kde 1 je nejvyšší společný dělitel těchto čísel. Protože jsme v Z133, tak víme, že
je kongruentní s 0 a tedy y je multiplikativní inverzí čísla 15 v Z133.
Celý postup vypadá takto:
Již zmíněné poslední rovnosti () se říká Bezoutova rovnost.
Protože jsme v Z133, tak všechny násobky 133 jsou rovny nule, upravíme na
v Z133, k -62 přičteme pro krásu výsledku 133 a vyšlo nám 71. Platí, že
v Z133, jinými slovy 71 je multiplikativní inverzí čísla 15 v Z133.
Zápis do tabulky
Zde je již mnohem rychlejší se naučit vyplňovat tabulku tak říkajíc automaticky, než přemýšlet nad tím, jak to vlastně funguje a jestli člověk vůbec počítá dobře...(koeficienty 1 0 a 0 1 jsou výchozím nastavením)
Nejnižší společný násobek
Euklidův algoritmus nám také odpovídá na otázku, jaký je nejnižší společný násobek číslel A a B (lcm(A, B) - least common multiple), protože platí
Literatura
- VELEBIL, Jiří. Diskrétní matematika : Text k přednášce. Praha : [s.n.], 2007. 193 s.