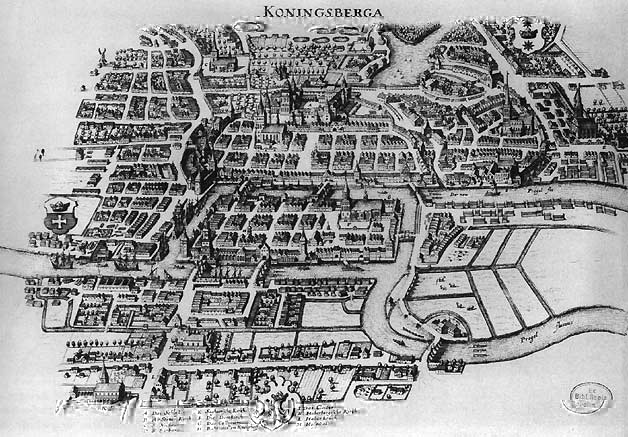
Město Královec (Königsberg, Kaliningrad) se rozprostírá na březích a ostrovech řeky Pregely. Mezi jednotlivými břehy a ostrovy vede sedm mostů (viz obrázek). Obyvatele města zajímalo, zda-li mohou při svých promenádách projít všechny mosty takovým způsobem, že se dostanou opět do původního místa, aniž by jednu spojnici přešli dvakrát.
Parafrází na tento problém jsou všechny dětské hry na domeček, hvězdu nebo prasátko jednou čarou (z nichž ne všechny lze vyřešit).
Řešení
Řešení přednesl v roce 1736 Leonhard Euler, čímž položil základ teorie grafů.
Věta: Neorientovaný graf lze pokrýt jedním tahem právě tehdy, pokud je souvislý a je Eulerův (má všechny uzly sudého stupně).
Věta: Nechť G je souvislý neorientovaný graf, který obsahuje právě uzlů lichého stupně (
), pak se každé jeho minimální pokrytí skládá z
otevřených tahů, z nichž každý spojuje dvojici uzlů lichého stupně.
Tyto dvě věty nám říkají následující. Pokud chceme obrázek nakreslit jednou čarou (a vrátit se do původního místa), pak musí z každého uzlu vycházet sudý počet čar. Pokud tomu tak není, tak potřebujeme tahů, protože to jsou ta místa, kde tužku zabodneme a kde jí z papíru zvedneme.
Z obrázku nyní vidíme, že obyvatelé Královce nejenže nemohou přejít mosty tak, aby přešli každý jednou a vrátili se do původního místa, ale úlohu dokonce nelze vyřešit ani při absenci požadavku na návrat do původního místa (je zapotřebí dvou tahů).
Literatura
- KOLÁŘ, Josef. Teoretická informatika. 2. vyd. Praha : Česká informatická společnost, 2004. 205 s. ISBN 80-900853-8-5.