Prohledávání do hloubky (depth-first search, DFS) je algoritmus určený k procházení grafu, který má široké uplatnění - jeho principů se využívá při zjišťování počtu komponent, topologického uspořádání nebo detekci cyklů daného grafu.
Princip
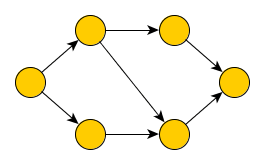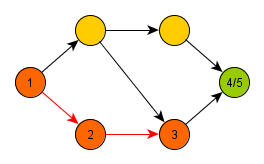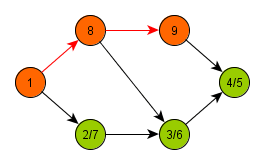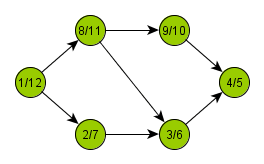
Algoritmus zvolí libovolný uzel a označí jej jako otevřený, zpracuje jej a zavolá sám sebe na všechny dosud neobjevené potomky daného uzlu. Po návratu z rekurze uzel označí jako uzavřený. Tímto způsobem dojde k průchodu všech větví grafu do maximální hloubky.
Složitost
Za předpokladu, že lze přistoupit k sousedům daného uzlu v konstantním čase, tak je asymptotická složitost tohoto algoritmu , protože projde každým uzlem i hranou právě jednou.
Kód
/**
* Dosud neobjeveny uzel
*/
private static final int FRESH = 0;
/**
* Otevreny uzel
*/
private static final int OPEN = 1;
/**
* Uzavreny uzel
*/
private static final int CLOSED = 2;
/**
* Prohledavani do hloubky (rekurzivne)
*
* @param graph
*/
public static void depthFirstSearch(GraphIface graph) {
//Stavy jednotlivych uzlu
int[] state = new int[graph.getVertexCount()];
for (int i = 0; i < state.length; i++) {
state[i] = FRESH;
}
//zajisti pruchod vsemi komponentami souvislosti
for (int i = 0; i < graph.getVertexCount(); i++) {
if (state[i] == FRESH) {
doDFS(graph, i, state);
}
}
}
/**
* Provede prohledavani do hloubky
*
* @param graph graf
* @param vertexNr cislo uzlu
* @param state stavy uzlu
*/
private static void doDFS(GraphIface graph, int vertexNr, int[] state) {
state[vertexNr] = OPEN;
List<GraphNodeIface> succ = graph.getNode(vertexNr).getSuccessors();
for (GraphNodeIface n : succ) {
if (state[n.getId()] == FRESH) {
doDFS(graph, n.getId(), state);
}
}
state[vertexNr] = CLOSED;
}
/**
* Operace, ktere by mel splnovat graf
*
* @author Pavel Micka
*/
public interface GraphIface<ENTITY> {
/**
* Prida hranu do grafu
*
* @param from uzel, ze ktereho hrana vychazi
* @param to uzel, do ktereho hrana vede
*/
public void addEdge(int from, int to);
/**
* Vrati pocet hran grafu
*
* @return pocet hran grafu
*/
public int getEdgeCount();
/**
* Vrati uzel s danym identifikatorem
*
* @param id
* @return
*/
public GraphNodeIface getNode(int id);
/**
* Vrati pocet vrcholu grafu
*
* @return pocet vrcholu grafu
*/
public int getVertexCount();
/**
* Odstrani hranu, v pripade vicenasobneho vyskytu odstrani prvni vyskyt
*
* @param from uzel, ze ktereho hrana vychazi
* @param to uzel, do ktereho hrana vede
*/
public void removeEdge(int from, int to);
/**
* Operace, ktere by mel splnovat uzel grafu
*
* @param <ENTITY>
*/
public interface GraphNodeIface<ENTITY> {
/**
* @return the id
*/
public int getId();
/**
* @return the successors
*/
public List<GraphNodeIface> getSuccessors();
/**
* @return the value
*/
public ENTITY getValue();
/**
* @param value the value to set
*/
public void setValue(ENTITY value);
}
}
Literatura
- KOLÁŘ, Josef. Teoretická informatika. 2. vyd. Praha : Česká informatická společnost, 2004. 205 s. ISBN 80-900853-8-5.
SEO od společnosti Digital Pylon
Online casino s algoritmem
České casino online online slot-vegas.cz
Hrajte nejlepší hry jako je GoodGame Empire.
Zajímavé články: Jak najít práci snů? Zvolte kariéru v IT!, Češi mají rádi hrací automaty online, Jak funguje algoritmické obchodování Casino, Online výuka Algoritmus a online marketing mají svá pravidla, Automaty, Matematický vliv, Ratings, Jak fungují algoritmy hazardních her online: více znalostí, více peněz, SYPWAI - nástroj pro vědecký vývoj, Vynikají na globálním trhu: Nejlepší vývojáři softwaru pro online výherní automaty, Jak si vybrat nejlepší české online casino, Proč byste měli hrát online casino VPN revoluce, Kde najdeme algoritmy v každodenním životě?, Čeká vás pracovní pohovor mimo město? Podívejte se, jak dokonale zvládnout včasný příchod, 5 úžasných technologií ze světa hazardních her, Mirror and access to Mostbet, Svou kancelář můžete mít stále po ruce, Jaké výhody má digitalizovaná firma oproti off-line konkurenci?, Jaký systém vybrat pro snadné řízení výroby?, Nahradí umělá inteligence ajťáky?, Důvody, proč používat SnapTik ke stahování videí TikTok, Dokonalý den na pláži: Co si vzít s sebou, aby byl výlet zábavný a bezpečný?, Jak přežít dlouhý let?, Go pay GoodGame Empire, Blockchain, Rozhovor, Umělá inteligence, Ochranná známka pre softvér: Prečo ju registrovať?, Role kryptografických algoritmů v zabezpečení online kasin, Jaké jsou náklady na nákup 3D tiskárny?, Jak algoritmy vylepšují online zážitky v roce 2025, Epilace laserem a péče o pokožku před a po ní, Byty k pronájmu Sokolov - výhody a rizika pronájmu bytu bez realitky, Filmy a seriály plné hádanek: kryptografie jako hlavní téma, Kdy obnovit data z disku běžně dostupným softwarem a kdy už se obrátit na profesionály?, Jak se zbavit jizev po akné? Co z domácí péče opravdu funguje? Na co všechno se zaměřit při výběru internetového připojení pro firmy?, Promo kód casino: mezi matematikou bonusů a českou realitou